Stand van de Markt – 22 : “Random is predictable”

Beste Lezer,

Eén van de contra-intuïtieve weetjes uit de probabilistiek, een discipline uit de statistiek, is dat hetgeen willekeurig is, eigenlijk volmaakt voorspelbaar is.

Wel eerst even goed afspreken wat we bedoelen met “willekeurig”.

Willekeurig betekent dat het aleatoir is. Of in het Engels “arbitrary”.

“Random“, dat ik in mijn titel gebruik, is eigenlijk géén juiste vertaling van willekeur (maar het klonk beter in mijn titel ;-).

“Random” is iets anders. Het is het outlier resultaat, de uitkomst die niet past in het schema van de voorspelde mogelijke uitkomsten. Random is de Black Swan van Nassim Taleb. Daarover meer een volgende keer.

Hier gaat het dus over willekeur. Het “aleatoire”.

Het type-voorbeeld is de uitkomst van een dobbelsteen (een “alea”). Of van het balletje op de roulette-tafel in het casino.

En wat zeg ik daar nu over ?

Welnu, ik zeg dat iets dat willekeurig is, zoals de uitkomst van dobbelstenen of een roulette-tafel, eigenlijk volmaakt voorspelbaar is. Het is willekeurig en daarom voorspelbaar.

Dat is al behoorlijk contra-intuitief. Dat klinkt raar.

Maar omgekeerd kan ook, en klinkt nog straffer :

Wanneer iets niet voorspelbaar is, maar dan ook écht niet voorspelbaar, wel, dan is het, per definitie, niet willekeurig.

Of deze : opdat iets werkelijk onvoorspelbaar zou zijn, is het mathematisch (!) vereist dat het om niet-willekeurige processen gaat.

Onvoorspelbaarheid vereist immers net de afwezigheid van willekeur. Zodra de processen willekeurig zijn, worden ze voorspelbaar.

En die voorspelbaarheid van willekeurige processen leidt ook tot hun beheersbaarheid.

Willekeurige processen zijn immers beheersbaar omdat ze voorspelbaar zijn. Wanneer je, zoals in een puur willekeurig proces, de uitkomst kan voorspellen, bijvoorbeeld weet wie gaat winnen en wie gaat verliezen, kan je dat beheersen.

(wie mij (nog) niet gelooft moet zich even afvragen hoe het komt dat in de casino de bank altijd wint)

Een willekeurig proces is dus ook niet zo gevaarlijk. Het is voorspelbaar en dus beheersbaar.

Het zijn juist de niet-willekeurige processen die gevaarlijk zijn. Het is enkel in die niet-willekeurige processen dat je enorme onvoorziene verliezen kan lijden.

Dit is allemaal erg contra-intuïtief en verdient dus wat toelichting.

De “normale distributie” van willekeur

Zoals ik al eens besprak in SvdM 15 (Stand van de Markt – 15 : The Index of Fear) kan je de resultaten van een puur willekeurig proces, zoals bijvoorbeeld het gooien van twee dobbelstenen, op een grafiek zetten.

En die grafiek ziet er dan zo uit :

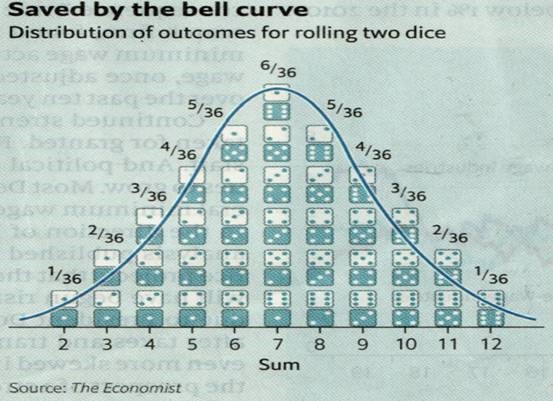
Als je twee dobbelstenen gooit, heb je in totaal 36 verschillende mogelijke uitkomsten.

Dat zijn de 36 setjes van telkens twee stenen op de grafiek.

Maar niet alle combinaties hebben evenveel kans om voor te komen.

Als je bv. 5.000 keer (“wet van de grote getallen”) met twee dobbelstenen gooit ga je verschillende keren een totaal van 7 gegooid hebben, ook een aantal keren 6 en 8, maar veel minder 2 of 12.

Dat is omdat je met twee dobbelstenen in zes mogelijke combinaties een totaal van 7 kan gooien (6+1, 5+2, 4+3, en ook 1+6, 2+5, 3+4), en in vijf combinaties een totaal van 6 of 8, maar je kan maar op één manier een 12 gooien of een 2.

Die grafiek verdeelt die mogelijke resultaten op een “normale” manier. Dit heet een normale distributie.

(Voor het balletje op de roulette-tafel, is de grafiek, na een groot aantal worpen, veel eenvoudiger : de helft op zwart en de helft op rood; ook voor één dobbelsteen is de grafiek eenvoudig, nl. alle uitkomsten 1/6de keer)

Eén van de vereisten van zo een normale distributie is dat de willekeur “puur” is. Het proces moet “puur aleatoir” zijn.

In deze context betekent dit dat de variabelen niet met elkaar correleren. Er is geen enkel verband tussen de 132ste worp en de 133ste. Elke worp geeft telkens opnieuw een puur willekeurig resultaat.

In gewoon Nederlands: de kans dat je dit keer een 12 gooit wordt in niets beïnvloed door wat je eerder gegooid hebt.

Ook de kans dat je kop of munt gooit, of rood of zwart op de roulette-tafel, is elke keer opnieuw puur willekeurig bepaald (en dus telkens opnieuw 1 kans op 2). En dit ongeacht wat je eerder gegooid hebt.

En dus ook ongeacht het feit dat je net 17 keer achter elkaar, telkens opnieuw, altijd “munt” gegooid hebt.

In tegenstelling tot popular belief is ook de 18de keer de kans op “kop” nog steeds gewoon 1 op 2 !

Nogal wat mensen begaan daar een vergissing.

Zij denken dat er nu statistisch een hogere kans bestaat om (eindelijk) “kop” te gooien.

Maar dat is niet juist. Een dobbelsteen, of een muntstuk, of roulette-balleke, heeft geen geheugen.

Hij herinnert zich niet hoe hij net gevallen is.

De distributie is dus normaal omdat de willekeur effectief puur is.

Er bestaat tussen de opeenvolgende worpen geen beïnvloeding, geen causaliteit, geen correlatie, geen feedback-loop, geen interactiviteit.

Wat zijn de kenmerken van zo een normale distributie ?

Zo een normale distributie heeft twee kenmerken die handig zijn : (a) je kan voorspellen wat de eind-uitkomst zal zijn, tenminste over grote aantallen, en (b) je kan een betekenisvol gemiddelde berekenen dat je toelaat om een inschatting maken van het risico op afwijking t.o.v. dat gemiddelde.

a. Voorspellen van de eind-uitkomst

Dat voorspellen van de eind-uitkomst lichtte ik al toe. Dat is de grafiek met de verschillende dobbelsteen-combinaties.

Zolang je maar een voldoende groot aantal keer met die dobbelstenen gooit (“law of large numbers”) gaan de uitkomsten zijn zoals op de grafiek.

Als je 36.000 keer gegooid hebt, zal je 6.000 keer in totaal een 7 gegooid hebben, 3.000 keer in totaal een vier, en 1.000 keer een 12.

Gegarandeerd.

En dit is dus, dat had u al begrepen, de verklaring waarom in het casino de bank altijd wint.

Willekeur is voorspelbaar.

b. Betekenisvol gemiddelde – standaarddeviatie – risico-inschatting

Een tweede kenmerk van een normale distributie is dat het je toelaat om een betekenisvol (of relatief “stabiel”) gemiddelde te berekenen.

En enkel een betekenisvol gemiddelde kan gebruikt worden als referentie-punt om aan risico-berekeningen te doen.

Met andere woorden, een normale distributie (resultaat dus van pure willekeur) laat toe om zinvolle risico-inschattingen te maken.

Een voorbeeld :

Stel dat de gemiddelde grootte van volwassen mannen in Vlaanderen gelijk is aan 182 cm.

(ik vrees dat het ondertussen wel eens meer zou kunnen zijn, maar goed, ik schrijf dit artikel, niet uw of mijn zoon….)

De grootte van volwassen mannen is “normaal verdeeld”, zoals de worp van twee dobbelstenen.

Je hebt de meest voorkomende uitkomst, en dan een (beperkte) afwijking ten opzichte van die uitkomst.

Die afwijking van die model-uitkomst heet de standaarddeviatie. De metrische eenheid van een standaarddeviatie heet “sigma”.

Stel nu – het zal ongeveer juist zijn – dat voor de volwassen mannen in Vlaanderen één standaardafwijking (“sigma”) ten opzichte van het gemiddelde gelijk is aan 8 centimeter.

Omdat we in een normale distributie zit krijg je dan deze verdeling :

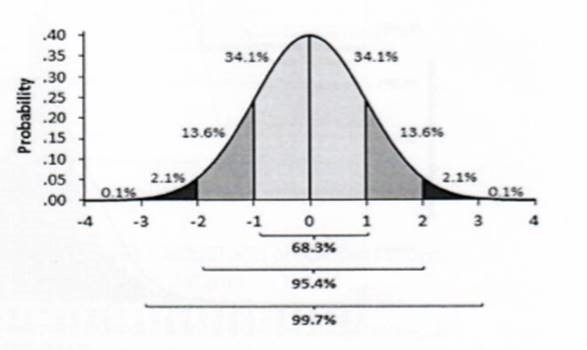
De cijfers van 1 tot 4 (of van -1 tot -4) op de horizontale X-as staan voor het aantal standaardafwijkingen.

De probabilistiek leert ons dan dat in dat geval 68% van de mannen in Vlaanderen tot maximum 1 standaard-afwijking (dus 8 cm in plus of min) groter of kleiner is dan die 1,82 meter. En 95.4 % is tot maximum 2 afwijkingen, dus 16 cm, groter of kleiner dan dat gemiddelde.

Mannen die nog méér dan twee sigma-eenheden (dus meer dan 16 cm) afwijken van het gemiddelde, >2-sigma guys, zijn dus kleiner dan 166 cm of groter dan 198 cm (statistisch kan dit nog voor 2 x 2.1% van de mannen).

“3 sigma guys”, dus kleiner dan 158 cm of groter dan 206 cm worden statistisch erg onwaarschijnlijk (0.3%).

Meer dan 4 sigma (een afwijking van meer dan 32 cm tov 1.82 meter) is statistisch ondenkbaar.

In zo een normale distributie heeft het gemiddelde dus een betekenis.

We kunnen daar iets mee. Het is de “norm”. Het is “normaal”. En dus kunnen we het gebruiken om berekeningen te maken over de kans dat een volwassen man in Vlaanderen x-aantal cm groter of kleiner is dan dat gemiddelde.

Of in een andere context, over het “risico” dat feit A of B zich voordoet.

Het gemiddelde is ook stabiel

In zo een normale distributie is zo een gemiddelde niet enkel betekenisvol en bruikbaar, zoals zonet gezegd, maar het is ook stabiel.

Een stabiliteit die natuurlijk bijdraagt tot zijn zinvolheid en bruikbaarheid.

Met stabiel bedoel ik dat het niet makkelijk verandert. Het beweegt niet.

Zelfs als ik in mijn sample van 10.000 volwassen mannen in Vlaanderen toevallig de grootste man van Eernegem zou overgeslagen hebben, is dat niet zo belangrijk. Zet die persoon er wél bij, met zijn massieve 2,10 m, en mijn gemiddelde gaat niet veranderen (of pas verschillende cijfers na de komma).

Dat is omdat “véél groter dan de rest”” nog altijd niet zo veel groter is. Mijn gemiddelde is een stabiel cijfer en daarom dus bruikbaar. Omdat de verdeling normaal is en iedereen zich in een beperkt veld daarrond beweegt.

Dit is erg verschillend van bijvoorbeeld de rijkdom van mensen in de wereld.

De rijkdom van mensen is niet “normaal verdeeld”.

(dit is geen politieke opmerking maar een probabilistisch gegeven).

De gemiddelde rijkdom van 10.000 mensen is geen betekenisvol of stabiel cijfer.

Als bij die 10.000 mensen uit mijn sample Bill Gates even komt aanschuiven, verandert het gemiddelde dusdanig, dat in feite alle 10.000 mensen eronder zitten (en alleen Bill Gates erboven). Dat is omdat de outlier exponentieel veel groter is. Onvergelijkbaar veel groter.

In een niet-normale distributie is het gemiddelde dus onbruikbaar, onstabiel en niet dienstig om standaarddeviatie-grafieken te maken.

En dus kan ik er ook niets mee doen om op een zinvolle manier risico in te schatten.

De gemiddelde rijkdom van 10.000 mensen, of 100.000 mensen, zegt ons niets over de kans/risico op een Bill Gates, en over hoeveel keren rijker dan het gemiddelde die dan wel maximaal kan zijn.

Waarom vertel ik dit nu allemaal ?

Ik vertel u dit omdat teveel mensen nog de beurs gelijkstellen met een casino.

Maar dat is, jammer genoeg, niet juist.

If only…

Ah ja, want in een casino, – een puur willekeurig proces -, worden de resultaten normaal verdeeld en zijn dus de uiteindelijke uitkomsten, wanneer de aantallen voldoende groot zijn, voorspelbaar en dus beheersbaar.

Al wat we nodig hebben is een puur willekeurig proces (geen beïnvloeding, geen correlatie, geen causaliteit) en een stabiel gemiddelde dat zinvol referentiepunt kan zijn (omdat het veld beperkt is : rood/zwart; kop/munt; 11 mogelijke combinaties met twee dobbelstenen).

Als echter de verdeling niet normaal is, bijvoorbeeld omdat het proces niet puur willekeurig is, wordt het onvoorspelbaar, en dus onbeheersbaar en dus gevaarlijk. Omdat je in niet-normale distributies, zoals rijkdom van mensen, enorme outliers kan krijgen.

Laat de beurs nu net een ander voorbeeld zijn van zo een niet puur willekeurig proces.

Op de beurs wordt wat op dinsdag gebeurt wél beïnvloed door wat hij op maandag gedaan heeft. En door 7.000 andere factoren die allemaal op elkaar inwerken, elkaar versterken, of elkaar compenseren, enzovoort.

Er is dus wél correlatie, wél causaliteit, wél interactiviteit en er zijn verschillende positieve en negatieve feedback-lussen.

En dat belet ons om daar zinvolle risico-inschattingen over te maken, met statistisch correcte kansberekeningen dat de beurs met één of twee of drie standaarddeviaties kan zakken of stijgen. Of om uitspraken te doen over de statistische quasi-onmogelijkheid van een >4-sigma verlies.

De verdeling van alle mogelijke uitkomsten op de beurs is immers niet normaal en de afwijkingen t.o.v. het “normale” kunnen verschillende keren groter zijn. Er bestaan “abnormaal” grote bewegingen. Probabilistisch gesproken zijn er geen grenzen aan de mogelijke bewegingen. Er is een risico op enorme “outliers“, de zgn. Black Swans, de random events.

(Wanneer dat dan toch in een distributie-model geduwd wordt, heeft men het over een “long tail distribution system”, dus een grafiek zoals hierboven maar dan met een lange “staart” aan de linkerkant naar -5, -6, -7 enzovoort. In theorie ook aan de rechterkant, maar links is waar verlies geleden wordt en dus waar iedereen op focust. Vandaar ook “left tails”. Als die staarten dan ook nog eens dik zijn, dus met een hogere kans dat het gebeurt, heb je “fat tails”)

De beurs is dus onvoorspelbaar en gevaarlijk, niet omdat het een casino is, maar juist omdat het niet een casino is.

Wat is de beurs dan wel ?

Een complex adaptief systeem (“CAS”).

Een complex adaptief systeem heeft een aantal kenmerken, die we volgende keer gaan bespreken, maar het meest opvallende kenmerk is de niet-lineariteit. Ook wel genaamd de “exponentialiteit“.

Het is die exponentialiteit die de uitkomsten zo buitengewoon afwijkend maakt. Die de tails zo long and fat maakt.

En dus gemiddelden maakt die waardeloos zijn, omdat ze niet stabiel zijn.

En dus ook standaarddeviaties vastlegt die geen betekenis hebben.

En dus ook risico-inschattingen genereert die er volledig naast zitten.

In a non-linear system you’re on your own.

Dat bespreken we de volgende keer.

* * *

That’s the news.

Steady as she goes. 😊

Cheers !

Arne